| Adapted for the Internet from: Why God Doesn't Exist |
| Riemann's warped triangle |
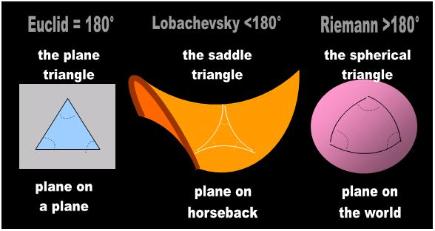
- 1.0 Riemann’s Triangle: The triangles and circles of relativity are warped
- Relativists use the infamous Riemann Triangle analogy to make their case for yet another misconceived dimensional aspect of
their beloved space-time. In the 19th Century, Riemann discovered that if he bent Euclid’s flat triangle around the surface of a
sphere, the internal angles add up to more than 180º (Fig. 1):
- “ There is no escaping it: there is a triangle whose angles sum up to more than 180º.” [1]
2.0 Objections to the warped triangle analogy
I have the following objections to the misconceived Riemann Triangle analogy.
a. A Riemann Triangle is not a triangle
One shortcoming of Riemann’s triangle is that it is not a triangle. A triangle has angles and is a member of a category of
figures called planes. Riemann’s contraption meets neither criterion, but the mathematicians prod on like bumbling fools.
Definitions mean nothing to them. The rules are there to be tweaked as necessary to accommodate their theories.
b. The Riemann analogy requires prior experience in a higher dimension
Another troubling aspect of Riemann-like explanations is that the Flatlander would be unable to certify that the
diameter-varying circle theory is true. Relativists are assuming that the Flatlander was once living on a circle where π was
a constant and later traveled to a sphere where π allegedly shrinks. The Flatlander is bearing down on the issue from a
priori knowledge. For the sake of their mental health, I hope the mathematicians are not suggesting that they also traveled
to the fourth dimension and back.
c. Relativists amend well-established definitions to accommodate their theories
In order to get their Riemann argument across to the uninitiated, relativists are compelled to amend well-established
definitions. Euclid defined a circle as a plane and a diameter as a straight line (not as an arc).
- “ A circle is a plane figure... A diameter is a straight line.” (Bk. I, Defs. 15 & 17) [5]
“ circle: a plane closed curve line… A diameter of a circle is the line segment
through the center of the circle and having both end points on the circle…
the area of a circle… area: the surface of any plane geometric figure” [6]
The mathematicians appear to be talking, rather, about a patch of snow capping the peak of a mountain. Apparently, in
relativity, a circle can be anything that looks like a pancake, a funnel, or a hemisphere, and a diameter can just as well be
a line bent around a soggy pizza or a string stretched around a basketball (Fig. 3).
Fig. 1 Plain stupid: Relativistic triangle angles |
Euclid defined a triangle as a plane having three angles. Riemann’s triangle has neither of these two properties. It is not a plane and certainly has no angles. An angle is by definition circumscribed to planes. |
The mathematicians extrapolate Riemann’s argument to persuade you that a Flatlander can infer the existence of higher
dimensions by taking measurements in his local region of space. For example, a Flatlander who draws a series of concentric
circles on a sphere will observe that the diameter progressively increases in relation to its circumference (Fig. 2):
- “ In this way creatures which cannot leave the spherical surface, and cannot even
peep out from the spherical surface into three-dimensional space, might discover,
merely by experimenting with discs, that their two-dimensional ‘space’ is not
Euclidean, but spherical space.” [2]
[How does a square sit flat against the surface of a sphere? Isn’t his left corner already
‘peeping out’ of 3-space? If we mold the square so that it sits everywhere against the
surface, can we continue calling it a square or should we call it a carpet?]
“ We thus discover by measurements carried out on the surface of the sphere that this
surface is not a plane.” (p. 89) [3]
“ the inhabitants of the surface of a sphere can soon discover that they are not living
in Euclidean space. When they draw a circle on the ground they will find that the
circumference is less than 3.14159… times the diameter. Similarly, in drawing
triangles they will see that the three angles add up to more than 180º. From such
measurements they will conclude that their space is curved” (pp. 71-72) [4]
- […then they were never Flatlanders to begin with! The scenario was 3-D from the start.]
Thus, without actually experiencing it, the relativist claims that a Flatlander can figure out strictly through the measuring
process that there is a higher dimension (i.e., that the universe is not 2-D, but rather 3-D). It is relying on a mixture of
measurement, math, analogy, and a far stretch of the imagination that relativists believe that, despite being unable to
experience it directly, they can infer the existence of a fourth dimension or tell us whether our Universe is open, closed, or
flat.
Fig. 2 The warped circles of relativitys |
Relativists owe many of their amusing conclusions to tender definitions. Of course, it shouldn’t surprise you when they
arbitrarily modify these definitions to accommodate their idiotic theories or that they later have trouble answering simple
questions asked by kindergarteners:
- “ Question: since one of the parts to Euclidean Geometry is that the relation between
a circle's circumference and its diameter (pi) is always 3.1415926535897923...
doesn’t that mean that the value of pi changes when space is curved?
Answer: What happens on the surface of a sphere? Instead of straight lines, we
have ‘geodesics’…if ‘pi’ depends on the radius of the circle, then the ratio of
circumference to diameter is not fixed, and if the ratio isn’t constant, there is no
meaning in the definition of pi as THE ratio of circumference to diameter.” [7]
Another conceptual shortcoming of the Riemann analogy is that relativists confuse objects with motion and nouns with
verbs. A straight line is a static object. A geodesic is an itinerary (dynamic concept). The fools of relativity perceive a
diameter not as a dirt road, but as a series of steps along a dirt road. They incongruously state that this itinerary is
‘straight’. However, for the purposes of Physics, straight is an adjective and may only be used to qualify physical
objects. If a line is straight, it may touch a sphere at a single location. We call this particular line a tangent. In science,
it is irrational to qualify a geodesic with the adjective straight.
Perhaps the mathematicians would rather argue that their infamous ‘itinerary’ is rectilinear.
This proposal fails just as well. If the itinerary conforms to the surface of a sphere, the trajectory is at best curved like the
arc of a circle. There is only one way to travel along the surface of a sphere and it ain’t along a rectilinear path!
But these arguments pale when contrasted with the one that follows. An itinerary is a movie that consists of many frames.
In each frame of the movie every atom in the Universe has a different location. Every step you take, the Earth moves 30
kilometers around the Sun. It doesn’t seem that way because you reference your motion to seemingly static rocks, houses,
and telephone pole here on Earth. Most people are unaware that these objects perpetually change their location with
respect to the Moon, Jupiter, and the Andromeda Galaxy. Make no mistake: no object in the Universe may travel rectilinearly.
It makes no sense to say that a movie of a flying baseball was rectilinear. Are the frames of the unrolled film stretched out in
a straight line or piled up on top of each other? Rectilinear motion is a surrealistic concoction of Mathematics. In Physics,
there is no such notion as rectilinear motion. No object may travel ‘straight’ in our beloved Universe.
d. Relativists bend the planes to accommodate their theories
Relativists also seem to have trouble distinguishing between a plane and a surface. A plane is 2-D whereas a surface is 3-D.
The word surface belongs exclusively to our 3-D world of solids. In Physics, we cannot warp planes even by the tiniest
amount for fear of converting them into surfaces. The seemingly innocent technique of warping planes demands a third
dimension into which parts of a triangle or circle can encroach. The warping of planes not only violates the definition of plane,
but implies that we were contemplating a 3-D scenario from the start. Relativists routinely take this extra dimension for granted
in their dissertations and prod on like fools without regard to their initial assumptions.
e. A relativist is an individual who attempts to ‘prove’ shape
Yet a fifth problem with the relativistic Riemann analogy is that the mathematicians insist on inferring or proving structure
through measurement, i.e., motion. Ever since Eratosthenes calculated the size of the Earth, the mathematicians took it as
gospel that shape and dimensionality can be inferred through measurement. What they forget is that Eratosthenes’ example
proves the opposite. Eratosthenes assumed that the Earth was spherical. If the Earth would’ve had the shape of a hotdog
and Eratosthenes happened to live at the tip, his calculation would have been meaningless (Fig. 1). In Physics, shape
precedes measurement.
3.0 The mathematicians cannot live without a witness
Disney is one who insists on proving shape through measurement. He argues that we can prove whether a plane figure is
flat through careful observation or measurement:
- “ one cannot mathematically prove, as Euclid had asserted, that space is everywhere
‘straight’ or ‘flat.’ ” (p. 65) [8]
- [Right! Math is exclusively a quantitative language of symbols. It cannot help us infer
any qualitative aspect of nature. Math has absolutely nothing to do with the real,
physical world.]
- “ Whether it is or not can be determined only by careful observation or measurement …
Whether we believe our own space is curved or not must be determined by
experiment.” (p. 65) [9]
[Wrong! You don’t prove that a triangle or the surface of a table is flat with an experiment.
If a triangle is flat, it is so pursuant to the definition of the word flat! It either is or isn’t.
You don’t measure flatness. You define it! The mathematicians cannot live without their
beloved testimony! Regarding belief, you can believe anything you want. Whether you
believe that a bowling ball is flat or not doesn’t concern Physics. It concerns Psychology
and, in extreme cases, Psychiatry.]
Euclid and Disney are wrong because in science, and particularly in Physics, we are not in the habit of proving adjectives.
Only in Mathematical Physics do they kill the hours in this peculiar activity. In Science, we define adjectives before we use
them. An adjective is a conceptually motion-less, time-less word. It must be defined unambiguously if it is a strategic word
in the dissertation. It may be used only in the context of physical objects. A precise definition of strategic words distinguishes
ordinary from scientific language.
In a theory proposing that the Universe is flat, the adjective flat is absolutely indispensable. In a theory proposing that the
Earth is spherical, the adjective spherical is also indispensable. These theories would have no meaning unless we define
the words flat and spherical unambiguously. If a mathematician alleges that space is a physical object, he may point to a
mockup of space at the beginning of his presentation and describe it as being either flat or spherical. It doesn’t work the
other way around. It is unscientific for the mathematician to leave his mockup of space at home and tell you that he is
going to 'prove' that space is flat through a series of measurements he took. What is he going to prove? That the itinerary
of the leading edge of the tape was 180º? What if the members of the Spherical Cosmos Society refuse to accept his
impeccable findings? Is space not flat because a disgruntled interest group votes against his data? We don’t prove that a
board is flat by placing a level on it. A board is flat by definition. Whatever measurement we take only gives us a measure
of our level of ignorance. Hopefully, the Earth is flat, spherical, or cubic irrespective of whether we know this or not. If you
really want to ‘prove’ that space is flat or spherical, you must necessarily be standing outside of it! If you can’t be there
next to God, then you must absolutely make an assumption.
Adjectives belong exclusively to the stage of the scientific method known as the hypothesis. Mathematicians get into
trouble because they have the bad habit of using strategic adjectives at the step known as theory. This warrants that I give
you a maxim. If ever you hear a mathematician use adjectives at theory or beyond, you know that he is a moron. In fact, a
mathematician is a moron if he uses key adjectives at all to make a point during his lecture. An adjective is a qualitative
grammatical category that belongs exclusively to Physics. Mathematics is exclusively a language of quantitative adverbs.
It has no use for adjectives such as straight, continuous, or flat. It is the religion of Mathematical Physics which has
incongruously attempted to apply adjectives in the context of numbers. It is when the mathematicians provide physical
interpretations to their equations that they are forced to twist the language. It is when they give you a number for flat or for
straight that you should suspect their mental state. This is the point where their discipline converts to a religion.
To summarize, Riemann’s Triangle analogy fails every test. Relativists are not talking about a diameter, a circle, a plane,
or the 2-D, and neither are their arguments proof that we can infer a 4-D object through analogies or measurement.
Fig. 1 Crazy Al tottering on a hotdog |
Fig. 3 Crazy Al's warped diameter: π < π |

| Thank God we patched that hole in the mathematical Universe with a Riemann Triangle last night, Bill. Otherwise, the sun would shine through and we wouldn’t be able to get any sleep. |
| Euclid defined a circle as a plane. In the religion of relativity, a diameter apparently takes the form of the substrate the circle sits on. The mathematicians place a pancake on a ball and continue calling it a circle. This is how relativists end up with curved diameters and dimensions. Actually, they are not even talking about a straight line, but about distance traveled (geodesic). Euclid’s diameter is not a rectilinear path. It was never intended to be an itinerary. The original diameter was a static line that bisected (cut in half) a (2-D) circle (i.e., a ‘flat’ cross-section of a sphere). Al’s diameter is an attribute of a 3-D figure. The warped diameter of Mathematical Physics is a ‘dynamic’ property of the ‘curved’ surface of a sphere. Euclid’s diameter is a straight line on a flat plane that cuts a |
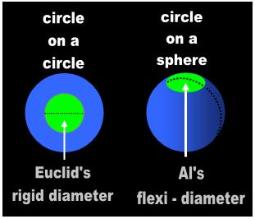
| sphere. Al’s diameter is an arc, the motion along the surface of a sphere. The diameter of Mathe-matical Physics runs perpendicular to the original diameter devised by the Greeks. In order to prevail with their idiotic Riemann analogy, relativists modified the original diameter to force fit the mathematical ‘geodesic’ into the picture. It is by introducing motion in lieu of a static line that Al’s boys ended up with the ludicrous notion that π is a variable! |

| You cannot determine the shape of the enormous object you’re standing on by measuring a tiny region of it. Eratosthenes ‘assumed’ the Earth was spherical, measured a region, and estimated the size of the sphere. He did not determine that the Earth was spherical by taking a measurement. If the Earth happened to have the shape of a hotdog, Eratosthenes's calculations would have been worthless. The idiots at WMAP have not learned this basic lesson. They believe that their measurements prove that the Universe in which they live is flat. |
| According to relativity, a Flatlander measuring concentric circles on a sphere realizes that the diameter increases faster than its circumference (i.e., π is not a constant). The 3-D idiot of Mathematics boasts that a 2-D Flatlander can infer from this experiment that there must be a 3rd dimension. Pursuant to this method, relativists extrapolate and claim that they can infer the existence of a 4th dimension by taking measurements of space. That's what the morons at WMAP spend your tax dollars on. The root of the problem with the relativistic argument is that the mathematicians use their definitions inconsistently. Euclid defined a diameter as a straight line on a plane figure known as circle. The relativistic ‘diameter’ is a curve, an arc along the surface of a solid known as a sphere. Relativists confuse the straight line of Physics (static figure) with the geodesic of Mathematics (itinerary). The static line of Physics is a photograph. The dynamic geodesic of relativity is a movie. The mathematicians are comparing apples and oranges. Nevertheless, rectilinear itineraries are surrealistic mathematical concepts. In Physics, an itinerary is a movie and it makes no sense to say that the frames comprising a movie are straight or running rectilinearly, for I ask, ‘with respect to what?’ |

- Module main page: Analogies are for laymen?
- Pages in this module:
- ________________________________________________________________________________________
- Copyright © by Nila Gaede 2008
