| Adapted for the Internet from: Why God Doesn't Exist |
2.0 Can motion be rectilinear?
There two ways to use the word rectilinear. Rectilinear could refer to a static alignment or to motion. A series of footprints in
the sand can be said to be rectilinear. The itinerary of a ball can also be said to be rectilinear. In both cases, we absolutely
need to compare the trace against something that is straight. In order for the footprints to be rectilinear, we absolutely need
to place a straight edge next to them. With respect to the itinerary of the ball, the mathematicians conceptually do something
similar. They plot the locations of the ball on a chart. If the trace is parallel to a straight line, they call it a 'straight line,' by
which they really mean 'a rectilinear trajectory' (Fig 2).
| A mathematician confuses straight with rectilinear |


| As soon as I heard the shots, I flew as fast and as rectilinearly as I could! |

| I don't know about rectilinear, but those hunters certainly can't shoot straight! They barely nicked my left leg. |

1.0 Straight or rectilinear?
Before we can have a rational discussion about lines, we must first agree on our definitions. The purpose of this preliminary
\exercise is not to define words for the sake of defining or in order to protect our religion. The terms we use to communicate
ideas must be precise if want the other person to have a crisp understanding of our ideas. The presenter should use the key
words that make or break his theory consistently. Only then
do we have a scientific (i.e., rational) definition.
The word I would like to analyze and define is the adjective straight. What is the scientific definition of straight?
One way to zero in on a definition you can use consistently is to start by looking at the properties or attributes we usually
associate with a word. For instance, straight seems to refer to a physical object that is rigid, meaning, made of a single piece.
In order for a geometric figure to be straight it cannot possibly be made of parts, for how would we conceptualize a series of
components being straight otherwise. Is a series of tracks straight? Would you have to compare it against a straight line to
prove that it is straight? Indeed, we can absolutely guarantee that they aren't. A series of rocks can at best be aligned
rectilinearly. For the purposes of Science, if we are to use it consistently, an adjective may only be used in the context of
objects. A word that is used to qualify motion or alignment is classified as an adverb. A table may be straight. A series of
tables may at best be aligned rectilinearly. There is no such thing as ONE rectilinear table in Science.
When we consider parts, we are not alluding to a single object and qualifying the whole with an adjective. We are instead
referring to how the individual components of an object are lined up vis à vis each other. We are not saying that the object is
straight. We are saying that the pieces are lined up parallel to straight: rectilinearly. For this we must compare the alignment
of the components to something that is straight. Hence, the definition of straight precedes the definition of rectilinear. The
rule is: scientific adjectives always before scientific adverbs.
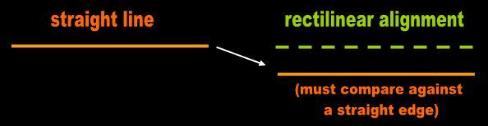
Fig. 1 Straight versus rectilinear |
| The adjective straight has at least two requirements. One is that it must qualify a physical object. The other one is that this object must be continuous: made of a single piece. For the purposes of Science, rectilinear is an adverb. This word cannot be used to qualify objects. It may only be used to modify a series of objects or displacement of one object. The individual is in effect placing a straight edge next to a series of objects or locations. |
However, in Physics, we cannot really get away with this. What the mathematicians are alluding to is a movie. So are they
going to unroll the film and spread the frames side by side in a given direction? Is this what they mean by a straight line?
In the real world, the Earth successively changes location with respect to every bit of matter in the Universe. Although you
seem to be standing still, you are actually traveling quite fast: 30 kilometers (18 miles) per second! That's the speed of the
Earth around the Sun. This means that the earthly ball also changes location with respect to every object in the Universe.
So what is the ball traveling 'straight' against? The Sun? The Moon? The Andromeda Galaxy?
Well, the mathematicians are aware of this, but they couldn't live with so much disorder. One fine day they decided to
hammer a stake in the middle of space and assign it a fancy scientific-sounding name such as 'frame of reference.' So
whenever a mathematician talks about a 'straight line,' he really means a rectilinear itinerary. The mathematician is talking
about a series of dots he plotted on a graph. Each one of these dots is not really a dot but a location, the location occupied
by the ball at a particular moment as it went from here to there. This 'straight line' implicitly invokes a coordinate system
known as a frame of reference. Without his goal posts, the mathematician is totally lost. He cannot measure his centimeters
and miles. He cannot talk about 'straight.' In his tiny mind, he cannot even talk about Physics.
However, in the real world, there is no such thing as a rectilinear itinerary. Both, the 'straight line' and the 'frame of reference'
are surrealistic concoctions of Mathematics. The mathematician in effect freezes the entire Universe and allows only his ball
(and hopefully himself) to move. The ball can thus move rectilinearly with respect to at least one straight edge because
everything is stand still. This enables the mathematician to take his measurements.
A perfect analogy for the ludicrous 'straight line' and 'frame of reference' of Mathematical Physics is an episode of The
Twilight Zone titled 'A kind of a stopwatch.' The guy uses a watch to stop time, but for unspecified reasons, he is the only
one free to move about. Yeah? No kidding?
In Physics, an object can move rectilinearly only if it is the sole entity in the Universe, in which case, ironically, motion is
undefined. Motion is defined as two or more locations as opposed to two or more positions of an object. This is yet another
example of the irreconcilable differences between Math and Physics.
If we now factor that replacing locations with dots and trajectories with lines has little to do with Science, the entire
foundation of Mathematical Physics disintegrates like a house of cards. The mathematicians inherited the amusing
habit of substituting the concept location with the object dot from traditional religions.
And just to throw another one in, if the mathematicians are alluding to motion, they can at best qualify their line not as
continuous, but as incessant: the incessant motion of a dot.
3.0 How is straight different than curved
So let's distinguish between objects and motion in order to use our terms consistently (i.e., scientifically). We will use the
adjective straight to qualify the architectures of objects and the adverb rectilinear to qualify how things are aligned. Unlike
in ordinary speech and religion, the word rectilinear may only be used as an adverb for the purposes of Science.
For the purposes of Science, it is also insufficient for that which is straight to be continuous. It must have direction as well.
If the edge of an object is continuous but does not have direction, it is known as a curve.
- straight (adj.): A continuous edge with direction. Straight is a specific type of edge.
curved (adj.): A continuous edge which lacks direction.
rectilinear (adv): 1. A series of footprints or marks which run parallel to a straight edge.
2. A series of locations occupied by one object which, when plotted, run parallel to a
straight edge. Rectilinear motion is surrealistic because it tacitly assumes that there is
a frame of reference (i.e., that the entire Universe has momentarily stopped moving).
- Curved edges are implicitly 'two-dimensional.' They necessarily encroach upon a second dimension. From an observer's
perspective, all curved shapes have width and height.
Contrast these definitions against the ones offered by the mathematicians:
“ A line can be described as an ideal zero-width, infinitely long, perfectly straight
curve (the term curve in mathematics includes 'straight curves') containing an
infinite number of points.s').” [1]
- In the religion of Mathematical Physics, straight and curved are synonyms. So what have we learned? How can the jury
understand the theory.
- 4.0 Conclusions
- Straight is an adjective and as such belongs exclusively to Physics – only physical objects can be conceived as being
straight. Mathematics has no use for adjectives. What quantitative meaning can the qualitative word straight have? As a rule,
if ever you hear a mathematician use an adjective in his presentation, you can tell him in his face that he is an idiot! A
mathematician who uses adjectives summarily converts the logical discipline of Mathematics into a religion known as
Mathematical Physics.
Fig. 1 Straight versus rectilinear |
| The adjective straight has at least two requirements. One is that it must qualify a physical object. The other one is that this object must be continuous: made of a single piece. The adverb rectilinear alludes to a series of objects or locations. These must be compared against a straight edge or line. |

- Module main page: A mathematician has no idea what a dimension is
This module: A mathematician confuses straight with rectilinear
- Pages in this module:
- ________________________________________________________________________________________
- Copyright © by Nila Gaede 2008
