Adapted for the Internet from:

Why God Doesn't Exist
In Science, it is
irrational to
attempt to
measure distance

    1.0   A mathematician is an idiot who believes that space has dimensions

    A mathematician stretches his tape from A to B and tells you that he just measured the distance between two objects.

    " The distance between two points in space can be ascertained with a rod, or a tape,
       or by optical means, and the result depends essentially on the physical behavior of
       the instruments used." [1]

    " mathematicians have devised numerous definitions of dimension for different types
       of spaces. All, however, are ultimately based on the concept of the dimension of
       Euclidean n-space E ⁿ. The point E ° is 0-dimensional. The line E ¹  is 1-dimensional.
       The plane E ²  is 2-dimensional.models" [2]

    " From the above geometric and physical arguments, we can conclude (not surprisingly)
       that space is three-dimensional" [3]

    A physicist knows better. The mathematician is simply telling us the length of his tape. Where in the world did the idiots of
    Mathematics ever get the idea that space has dimensions anyways?

    " Space, as we perceive it, is three-dimensional."  [4]

    " space is three-dimensional" [5]

    [Space has dimensions???? Bartender, I'll have whatever he had!]

    In Science, only physical objects may  have dimensions.

    The mathematician insists, this time with a clock. He sets it a-ticking while the cheetah runs and purports to measure
    space or distance or distance-traveled or whatever they call it in Math. He finishes timing the animal and gives you a
    value specified in meters per seconds or feet per minute. With a simple calculation, he converts this expression into a
    'distance.'

    You tell him that he has merely counted how many tiles he put in series on the floor. What he has done in effect with his
    calculation is add up the lengths of the tiles.

    The mathematician may try in other ways, but he will eventually learn what he never learned at the university. It is
    conceptually impossible to measure emptiness: space, distance, void, nothing. We can only measure physical objects.
    It is not space that has dimensions. It is the box or the floor or the tile or the tape that has dimensions (Fig. 1). From the
    idiots of Ancient Greece to the morons of today, the mathematicians of the world have never learned this fundamental
    lesson of measurement. Instead, they keep blabbing unscientifically about the dimensions of space, one-space,
    two-space, three-space, 11 and 26-space. It seems like the number of dimensions of space increases proportionally
    with the number of beers the bozos drink at the Math Club.

    As a last resort, the mathematicians may defend themselves saying that this is just a semantic issue.

    It is not. First of all, it is unscientific to say that space has dimensions, meaning that the volume a cube occupies is 3-D.
    Volumes are not 3-D. Cubes and spheres are 3-D. A cube is an object. A volume is a dynamic concept. Concepts do not
    have dimensions, especially if they are dynamic. Length, width,and height are static concepts.  Concepts are relations
    between objects.

    Nevertheless, the idiots of Mathematics believe today that space is made of particles. Therefore, I am not overdoing it.
    The mathematicians really perceive nothingness to have dimensions simply because they do not believe in absolute
    nothingness. If the mathematicians believe that the statement 'space has dimensions' is just a metaphor, they should
    not use it to communicate scientific ideas. They should leave poetry at the Literature class.

Fig. 1   The dimensions of space?
The mathematicians have
lost their minds. They
developed the most
incongruous language in
order to accommodate their
ludicrous theories. One of
their most stunning claims
is that space has dimensions.
In Science, only objects have dimensions. The dimension we call 'length' is not the
longest dimension as some mathematicians believe because dimensions have
nothing to do with size. They are strictly qualitative concepts. The dimensions are
named in reference to an observer. The width of an object runs horizontally, height
runs vertically, and length runs perpendicular to both of them. (Perpendicular is not
a quantitative concept of Math measured in degrees. It is a qualitative concept of
Physics. The word derives from perpendiculum, the plumb bob used by ancient
masons to gauge how crooked a wall was with respect to the horizon.)

Fig. 2   Length
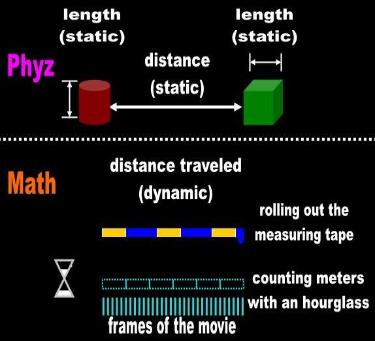
The mathematicians get confused with
the word length because they use two
irreconcilable definitions of this word
within the same dissertation. They
measure the extension of an object and
refer to this quantitative result as 'the
length of the object.' They also insinuate
that this meaning is equivalent to the
dimension known as length (as in length,
width, and height). It is not. Measured
length is a movie of the front end of an

    Actually, the mathematician is not even giving you the length the tape. He anchors one end of the tape and unrolls the
    rest so many yards or meters. From a conceptual point of view, he is again measuring the distance-traveled by the leading
    edge of the tape from its starting point (Fig. 2). The fact that he can take the reading with a clock (i.e., piecemeal) or express
    the results in terms of time (i.e., meters per second), indicates that measurement is a dynamic activity.

    In different words, the mathematician is measuring the rate at which the tile-layer lays tiles down. Think of the old nautical
    knot. The mathematician makes a standard, e.g., the meter. Then he checks his speed, e.g., 5 meters per second. Hence, if
    he travels 5 seconds, from a conceptual point of view, he has laid 25 tiles in a row or counted 25 knots or whatever. The
    ticks on a clock simply count how many rulers the mathematician has placed between his starting and ending location.

    The distance of Mathematics is actually the distance-traveled by a single object. The word motion is defined for a single
    object. When we talk about motion we are comparing the apple’s current location against its now imaginary origin. When
    an observer talks about motion and verifies distance-traveled he is relying on his memory. In the instant scenario, the
    mathematician is comparing a real entity (the leading edge of the tape) with an abstract location (the starting point of the
    leading edge of the tape).

    2.0   In Science, you can't measure length or distance

    These objections raise an even more fundamental question. Is it possible to measure genuine length or distance at all?
    Imagine speeding down a straight track on a train. How far are you from the end of the tunnel? How would you measure
    this distance if you can only conceive of and measure the distance between two objects horizontally or laterally
    (i.e., perpendicular to your line of sight)?

    The only way that a mathematician can measure distance separating him from the end of the tunnel up ahead is again
    dynamically, for example, by ricocheting signals off the far wall. Otherwise, he can measure this static distance in retrospect
    with a clock or by unrolling a measuring tape, which means that he had to define the standard first. The only way to define
    the 'length' standard is horizontally. In either scenario, the mathematician measures distance-traveled by one object
    (vertically). He is not measuring the static distance between two objects (Figs. 3, 4 and 5). Distance-traveled is a movie.
    Distance is a photograph. Thus, the paradox is that a mathematician can only measure static, horizontal distance through
    dynamic, vertical methods (unrolling a tape, laying tiles down, counting seconds, etc.). Again, Math and Physics don’t mix.
Look Bill! Let's see if I can make you understand. In our
beloved mathematical Hell, it is not the chair which has
dimensions. It is the space the chair occupies which has
dimensions. This is how we measured that your stretched
arm is a one-dimensional space.  Any more questions?

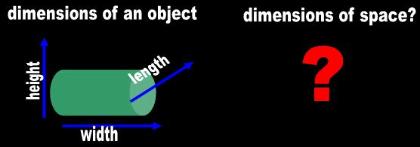
Fig. 3   Horizontal vs. vertical distance
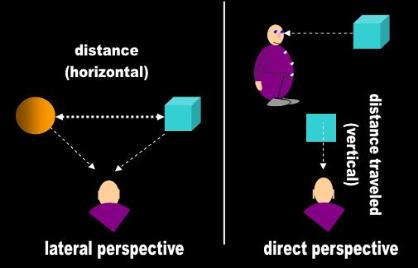
The distance of Physics is not measurable.
It consists of a qualitative gap between two
objects (horizontal distance).

The ‘vertical’ distance of Mathematics, in
contrast,  (i.e., the distance traveled by one
object) can only be measured dynamically.
When we measure the length of an object
or the distance between two objects, we
are in effect using a dynamic, vertical
method to measure a horizontal, qualitative
parameter. We are using a clock, laying tiles,
etc.
In Physics, we use the word 'distance' to
refer to the static gap that separates two
objects. We informally use the word
'length' to refer to the extension of an
object along any of the dimensions.
Formally, length is simply one of the
three dimensions.
Hey Newt?
What's Steve
doing?
Fig. 4

Distance from the
bserver's perspective
Yeah!  Let's walk!
If I don't travel a
distance soon, I will
poop on the length
of your shoes!
In order to know the
length of our
relation, we must
walk the distance,
my dear.
He's measuring the
dimensions of space.

    I'll run all that by again in different words. In Science, we can measure neither length nor distance. The length of Physics is
    the continuous matter lying between two surfaces. There is only one way to visualize this: horizontally. You must stretch
    the object in front of you from arm to arm and measure its length with a caliper or ruler. You can measure the length of an
    object only if it faces you sideways. The same occurs with distance. You must be staring at the two objects side by side
    and not in series, for then you would not be able to take a measurement. On the other hand, the distance-traveled of
    Mathematical Physics is always measured in series (vertically) (Fig. 3). It can only be measured after a horizontal standard
    has been established.

    Actually, it is much worse. From a conceptual point of view, what the mathematician has done is freeze the entire Universe
    and ensures that everything stands absolutely still (except for himself and the tape he holds in his hand). He hammers a
    stake in the middle of space and fixes a mathematical 'position' (what in Science is known as a location).  He refers to this
    surrealistic vision as a 'frame of reference' and tells you that it has something to do with Physics and with the real world.
    Now that things are properly anchored, he unfurls his tape from A to B, takes a measurement, and then allows the Universe
    to resume its regular movement. A good analogy of this mathematical idiocy is the Twilight Zone's episode titled 'A kind of
    a stopwatch'  You should watch it just to discover what the mathematicians of the world are into.

    The distance-traveled of Mathematics is a collage of sequential frames of a film pasted onto a photograph.The
    mathematician insinuates that he is talking about horizontal length and distance – which is what most people understand
    by the words length and distance – when he is really alluding to vertical length and distance (Fig. 4). The distant observer
    visualizes distance between two objects (Fig. 4) The traveler measures distance-traveled in his direction of motion (Fig. 5).
    The lengths and distances of Physics are static concepts (photographs). The ‘lengths’ and ‘distances’ of Mathematics
    involve time.


    3.0   Conclusions

    To recap, in Mathematics, there are no such concepts as length or distance. In Mathematics there is only distance traveled, a
    dynamic, quantitative relation. The mathematician makes a standard and specifies the length or distance of Physics in terms
    of so many units of this standard. The mathematician has devised several ways of measuring length:
    •   rolling out the tip of a measuring tape
    •   placing tiles in series and counting the number of tiles
    •   widening the opening of a caliper
    •   counting ticks with a clock
    •   ricochetting a signal and measuring speed or time with a clock.

    Mathematics has no use for the qualitative, static lengths and distances of Physics. The infamous 'distance' of Mathematics
    is in all cases distance-traveled, a dynamic, quantitative concept. The distance-traveled of Mathematics is an itinerary
    measured in meters or miles. It consists of a movie of the leading edge of a tape moving from here to there or of a ticking
    clock or some other dynamic method. The distance of Physics, in contrast, is between TWO objects. The alleged 'distance'
    of Mathematics consists of the trajectory of ONE object. The mathematicians are like stone masons, placing tiles on the floor
    to know the extent of the wall. Whether referring to length or distance, the mathematician measures dynamically and presents
    the results in terms of predefined units. A mathematician does not point to a photograph. He asks you to watch a movie. The
    mathematicians have no use for a 'qualitative' caliper. The tool they use to measure 'length' and 'distance' is a clock. However,
    unbeknown to them, they are not even measuring distance-traveled. They are measuring the length of the object they use as
    a standard. If a mathematician counts 5 tick marks on his clock, he has measured 5 of his standards as if they were one and
    still knows nothing about the 'length' of 'space.' The differences between the distance-traveled of Math and the distance of
    Physics is another example of how different these two disciplines are.

    As a result that the mathematician alludes to length, distance, and displacement with the word distance, he cannot use his
    definition of distance consistently (i.e., scientifically), for instance, to provide a physical interpretation to a phenomenon of
    nature. In extreme cases, this leads to ridiculous conclusions as exemplified by the 'space-like'/'time-like' idiot-talk of relativity.
Fig. 5

Distance- traveled from
the traveler's perspective
unrolled tape or the number of tiles the mason put in one hour. This 'length' is qualitatively
different than the 'static' length forming the triad of a 3-D object.

    ________________________________________________________________________________________


                                  Home                    Books                    Glossary            




        Copyright © by Nila Gaede 2008