06Triangle

1.0 The Euclidean triangle

uclid defined a triangle as a rectilinear figure contained by three straight lines.

In this context, t

he word

contained

means

that the three lines lie on the same plane for else we would have either a

pattern

opposed to a

figure

r the

figure is not

a plane

Thus formed,

the triangle encloses

as it name

suggest

three

angles.

This

definition

is consistent with the

requirement of the definition of

angle

that it be

formed on a plane.

What would the meaning of angle be if it

were gauged with lines occupying

different planes? What

would

the definition of a

degree

be in th

context

of curved lines

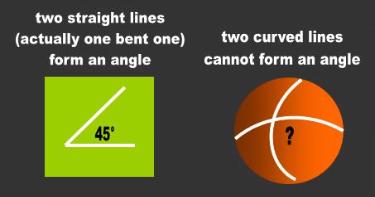
The mathematicians

get around

this

requirement

by drawing tangents to the curves.

For instance

, take

two curves that

intersect.

Since we cannot define

an angle between the curves, we artificially

place

two

straight

lines

on top of them and where they meet is the angle the curved lines have. The angle of two

curved lines is deemed to be the angle formed by two tangents to the curved lines.

This is how the idiots

of Mathematics extended

the concept of angles to

Riemann

Geometry. This technique masks the fact

that

an angle is still a plane pattern.

The

Riemann ‘triangle’

ith this groundwork we can now see why the relativistic Riemann triangle is not a triangle at all.

ecall that

the

Riemann

triangle

rests on the surface of a sphere which, according to relativists,

makes its internal

angles

add up to more than 180º. The problem is that Riemann’s ‘triangle’ lacks

the most important property

triangles: angles! Whether under Euclid's definition, present day

definition, or my proposed definition, an

angle is perceived to be on a plane. Riemann's

contraption does not rest on a plane

and it is misleading to

label it a triangle.

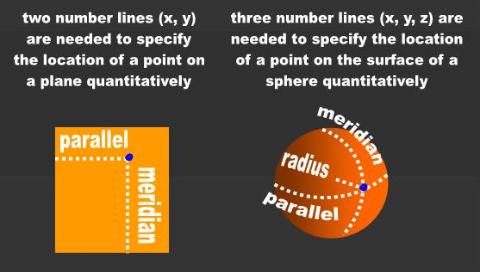
The traditional Euclidean triangle is a plane figure that has

two

dimensions

: width and height. In

Mathematics,

any point

can be specified with an ordered pair (

). the mathematicians call these variables

'dimensions' or

'coordinates.' In Science they are known as number lines, in turn known respectively as

parallel

and

meridian

A triangle can be thought of as a

cross-section of a pyramid

or a

cone.

location

on the alleged

Riemann

triangle,

on the other hand, must be

referenced using three

number

lines

known as parallel, meridian, and radius. It takes t

hree numbers

to specify

the location of a point on a

sphere

quantitatively

, which is where the mathematical physicists always place the Riemann triangle

. For

unknown

reasons, the mathematicians always forget the altitude or

radius

of the sphere, the

distance

traveled from the

center of the sphere to the point. This is the reason relativists regard

the surface of a

sphere to be two-

dimensional (2-D)

rather than 3-D

However, even if we only consider the shell

and not the solid (i.e., the ball), we still need to

specify the

distance from the center of the

sphere. A sphere is defined as all points equidistant from a

center

The

center

an integral

part of the

definition that the idiots of Mathematics

themselves

gave the sphere

The

mathematicians need the center of the sphere to define the sphere, but want you to believe that the center

not part of the sphere. The mathematical sphere is thought of as being hollow. The mathematical sphere

consists solely of the shell.

Therefore, pursuant to the mathematical definition of dimension

(number of numbers)

, Riemann’s alleged

triangle is 3-

" when two-space is curved into a third dimension, the angles always total either less than

180 degrees (if the curvature is hyperbolic, or 'open') or more than 180 degrees (if the

curvature is

spherical, or 'closed')." (p. 198)

[

]

A Riemann triangle is a peculiar slice of a sphere devoid of thickness. We cannot

manufacture

a Riemann

triangle because, despite that it takes up 3 dimensions it is not a 3-D

object. The Riemann

triangle is not a

triangle because it has no angles, either according to the

current definition of angle or

according to the

one

I propose here. An angle is formed by two

straight lines on an imaginary plane. The

Riemann ‘triangle’

doesn’t meet either criterion. A

Riemann triangle is constituted by curves, and there is no

dictionary that

defines angles in terms

of curves!

Indeed, pursuant to contemporary ‘constructions,’

triangles and circles

are not

geometric figures

but

rather

imaginary areas enclosed by

itineraries

that relativists

mistake for

boundaries. The

edges of all

geometric

figures of Mathematical Physics are

traces

of a moving point

paths

We are

watching a

movie

of a

bunch of

footprints

in the making.

The Riemann triangle fails the 2 requirements of a triangle. It neither has angles nor is it on a 2-D

plane.

angle is formed by straight lines. A Riemann Triangle is made of curves. A triangle is

defined as a flat

geometrical figure, i.e., lying or occupying no more than 2-D. The Riemann

Triangle

3-D. The R

iemann

triangle

not a solid because it has no width. It only has the ‘skin’ of a

sphere. But then we cannot look

any triangle

sideways and realize that it is a triangle. A

triangle can only be visualized head on. Without

the

sphere, the

Riemann triangle is nothing

(

Fig. 3

)

Fig. 1 Curved angles?

Fig. 3

I don't know, Bill. I've been
seeing them too. It must be some
unknown bug going around.

Fig. 2

Can we form an angle with curves?
Euclid defined an angle using
straight lines. The mathematicians
got around the requirement by
placing straight lines on curved
lines. The resulting 'angle' has the
magnitude formed by the vertex of
the straight lines. In this indirect
manner, the mathematicians were
able to extend the concept of
angles to curved lines. They
subsequently invented the curved
'tri' 'angle'!

You cannot see a Euclidean
triangle sideways

You can see a Riemann 'triangle
sideways because it is 3-D.
yet, you cannot manufacture a
Riemann triangle because it has
zero thickness!

The mathematicians require two number lines known as parallel and meridian to quantita-
tively specify a location on a plane, for instance on a rectangle. The mathematicians require
three number lines known as parallel, meridian, and radius to specify a location on a sphere.
For unknown reasons that the psychiatrists are still researching, the mathematicians never
include the radius. This in spite of the fact that they define the sphere as having a center. In
the religion of Mathematical Physics, a sphere is not 3-D, but rather 2-D.