The planes of
Mathematics are as
smooth as
sandpaper
Adapted for the Internet from:

Why God Doesn't Exist

    1.0   The Hausdorff space

    Is a plane made of points?

    Levy seems to think so:

    “ A set P (The Plane), whose elements are called points…a Hausdorff topological
       space.”   [1]

    So what’s a Hausdorff topological space, bright eyes?

    “ Topological spaces are structures that allow one to formalize concepts”  [2]

    The specific Hausdorff variant is:

    “a topological space in which points can be separated by neighbourhoods”  [3]

    The bottom line is that the Hausdorff topological plane is made of points, and the neighborhood Levy
    talks about has to do with points that surround a point, all of which add up to make a plane.

    But is he talking about a geometric figure such as triangles and circles? It certainly doesn't seem like
    it...

    “ the real numbers are a Hausdorff space…all metric spaces are Hausdorff.”  [3]

    Certainly, numbers have nothing to do with a triangle. We can’t define a circle with a set of numbers.
    We point to a circle and say circle. Only then does the ET understand the word circle. So what’s a
    metric space?

    “ In mathematics, a metric space is a set where a notion of distance between
       elements of the set is defined. The metric space which most closely corresponds
       to our intuitive understanding of space is the 3-dimensional Euclidean space. The
       Euclidean metric of this space defines the distance between two points as the length
       of the straight line connecting them.”  [4]

    In other words, the famous metric space has to do with distance traveled by one point. It is typically
    measured in terms of meters traveled. What do numbers and distance traveled by a point have to do
    with the geometric category known as planes? What does it have to do with Physics and the real
    world? Euclid’s successors visualize a plane as something comprised of countless points. And
    because in the religion of Mathematical Physics lines are also alleged to be made of points, this
    implies that a plane is made of countless lines as well.

    “ A finite geometry is any geometric system that has only a finite number of points.
       Euclidean geometry, for example, is not finite, because a Euclidean line contains
       infinitely many points, in fact precisely the same number of points as there are real
       numbers.”  [5]

    “a projective plane consists of a set of "lines" and a set of "points”  [6]

    Indeed, there is a theorem that says that a plane is made of the same number of lines as it is of points.

    “ It can be shown that a projective plane has the same number of lines as it has
       points. This number can be infinite (as for the real projective plane) or finite (as
       for the Fano plane).”  [6]

    [This is not a proof, as the idiots in relativity like to advertise. The conclusion follows
     from definitions. But as you can see, in the religion of Mathematical Physics, you can
     prove anything you want with numbers.]

    Fortunately, the proponents of projective geometry clarify that this has nothing to do with Physics or
    the real world.

    “ A projective plane is an abstract mathematical concept, so the "lines" need not be
       anything resembling ordinary lines, nor need the "points" resemble ordinary points.”  [6]

    So you wonder what this abstract mathematical exercise was all about? Why waste the energy on
    such rubbish? This type of idiotic analysis is what confirms to me that mathematicians are autistic
    morons. They should all be locked up!


    2.0   Manifolds

    The plane is also deemed to be a manifold:

    “ Differential geometry views a plane as a 2-dimensional real manifold” [7]

    So what’s a manifold, bright eyes?

    “ A manifold is an abstract mathematical space in which every point has a neighborhood
       which resembles Euclidean space”   [8]

    [Mmmmh. Must be a bad neighborhood! This neighborhood is also known as a
     topological space...]

    So what's a toplogical space, you insignificant ant?

    “ Topological spaces are structures... A topological space is a set X together with a
       collection T of subsets of X” [9]

    [Do not be fooled by the misleading word structure. In Mathematics there is no such
     thing as structure, meaning composition of objects: “Something made up of a number
     of parts that are held or put together in a particular way” [10]  The mathematicians had
     to change all definitions that stood in the way of their idiotic theories…]

    “ In mathematics, a structure on a set, or more generally a type, consists of additional
       mathematical objects that in some manner attach to the set”  [11]

    So what’s a set, you intellectual wimp?

    “ In mathematics, a set can be thought of as any collection of distinct things”  [12]

    [Unfortunately, the mathematicians have never defined the word 'thing' except as a
     synonym of object.]

    “ Set theory is the mathematical theory of sets, which represent collections of
       abstract objects…set theory provides the language in which mathematical objects
       are described…allowing mathematical objects to be constructed formally from the
       undefined terms of ‘set’, and ‘set membership’.”  [13]

    “ In common usage, a collection is any group of items that has one or more properties
       in common, usually brought together for some specific purpose…In mathematics,
       collection is not precisely defined, but can refer to various objects. Most often it refers
       to a set, class, family, or multiset.” [14]

    “ a class is a collection of sets (or sometimes other mathematical objects)” [15]

    So what have we learned after talking with these enlightened scholars?

    One thing we have learned is that it all comes back to this mysterious word object. As long as the
    mathematicians avoid defining this crucial word of Physics, they have absolutely nothing. Are they
    collecting love or pain? Is a set a group of souls or angels? Are the idiots gathering events or energy?
    What in the world are the mathematicians talking about?

    Well, whatever a manifold is, it certainly has nothing to do with Geometry or Physics. A manifold is an
    abstract watchmacallit. The planes of Physics have nothing to do with numbers. They are geometric
    figures. Numbers have to do with the verb ‘to count.’ As a figure, a plane is an object. It has shape. A
    number is always a concept: a relation. A number does not have shape.


    3.0   The genuine plane of Geometry is physically smooth

    If Euclid’s planes are made of discrete points, we must determine first whether the mathematician is
    referring to locations or dots.

    a.       If the word point means location, the idiots of Mathematics should call them
    locations so that the jury is not misled into believing that we are talking about
    Geometry and Physics. The mathematician cannot call his proposal a geometric
    figure to begin with. Is this infinite board made of locations? What shape do a
    million ethereal locations assume if we do not depict each with a dot? Can we
    talk about a flat ‘figure’?

    b.       If the mathematician is talking about discrete dots, we must first assume that
    ll dots have the same shape. Then we must determine which shape these dots
    have. Are they spherical, circular, cylindrical, cubic, squarish, or triangular?
    How do they sit elbow to elbow with each other in their ‘neighborhood’?

    Fortunately, we can at least eliminate the 3-D figures as models for planar dots. This means that we
    are going to construct our plane with planes: circles, squares, triangles, etc. In the incongruous
    religion of Mathematical Physics, we need to know what a plane is in order to construct (and thus
    define) a plane.  Isn’t Mathematical Physics fun!

    But these questions merely form the tip of the iceberg. In Fig. 1, I construct Euclid’s plane, first with
    circles and then with quadrilaterals just to make a couple of 'points.' Is it conceptually possible to
    construct a plane with discrete dots? Can such an ideal entity be smooth, continuous, and flat?  

    Castellanos rejects the circle,but accepts the square as a figure capable of tesselation.

    “ A Tessellation is a covering of an infinite geometric plane without gaps or
       overlaps by congruent figures of one type or a few types. In Euclidean Geometry,
       a square can be used to tessellate the plane; circles, however, will not tessellate
       the plane.”  [16]

    By definition a circle is a two-dimensional figure. Nevertheless, in order to avoid amending the
    definition of circle, and in order for the circle to continue being discrete, a distance must necessarily
    separate the edges of adjacent dots. So what should we call the interstitial region between dots?
    Is a plane a discontinuous figure riddled with holes?

    So let’s construct our plane with rigid tetragons. The question is whether the plane can be flat.

    The answer is that there is no way to guarantee flatness of the plane using discrete building blocks.
    In order for a plane to be ideally smooth, it must be made of a single piece: continuous. We simply
    cannot construct a flat plane with discrete objects or figures.

    Of course, if the entire plane was constructed dynamically by a single moving point, we cannot talk       
    of flatness at all. What we are watching is a movie, a raster being scanned on the screen in two
    dimensions. In this scenario, the mathematical plane amounts to an optical illusion. It exclusively
    relies on memory.

    To rap it up, if a plane is alleged to be ideally smooth, it cannot also be made of discrete points or of
    countless lines themselves comprised of discrete points. The points or lines would not lie on the
    plane, but would encroach instead on a third dimension. Such a surface would be rough if made of
    dots. Straightness can only be guaranteed if a figure is made of a single piece.
You see how smooth and flat
our relativistic world is, Bill?

Fig. 1   Crazy Al's rough and discontinuous planes
A. If a plane is made of circular
dots, what lies in the interstitial
regions between circles? Is a
plane full of holes or is it
conceptually smooth and
continuous?
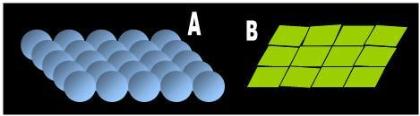
B. If a plane is made of quadrilateral dots, it cannot be flat. Each discrete, 2-D dot does not
occupy space; we can only visualize them head on. So how do we know that they are
perfectly aligned? Obviously, we cannot determine this through measurement. We can only
make an assumption. We can say that they are aligned by definition of the word plane.

This means that all the pieces occupy the same plane, which is the word that we are trying
to define.


    ________________________________________________________________________________________


                                  Home                    Books                    Glossary            




        Copyright © by Nila Gaede 2008