| QM’s ‘mother of all particles’ prevents SR’s ruler from disappearing if it travels at c |
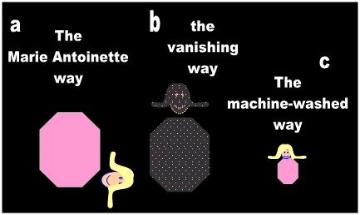
There are three ways that a boy may contract for ‘real’ (i.e., in the physical world). He can suddenly lose a chunk of his body
much the way Marie Antoinette surrendered about a foot off her shoulders during the French Revolution (Fig. 1a). However,
this barbaric method entails a loss of mass, which Einstein assures us either remains unchanged (rest) or increases
(relativistic) in near-c situations. Therefore, SR does not suggest that this is how a dynamic body contracts. Another way is
to compress each of the boy’s atoms. It is not the same to fill a box with the same number of half-blown as with full-blown
balloons. However, a more noticeable effect of this mechanism would be the ghostly disappearance of the boy, who would
gradually vanish as the space-to-matter ratio within the volume he occupies increases (Fig. 1b). Relativists are not suggesting
that this is what happens either. They propose, instead, that a boy shrinks the way my favorite pants shrink when my wife
accidentally washes them in hot water after an argument. The distances between atoms constituting the boy decrease and
his body occupies a smaller volume (Fig. 1c). This situation is unlike the previous scenario where the sub-micron
constituents of each atom shrink in situ and make the body a tad smaller. Here, the atoms are spaced closer together and
closer yet the faster the body travels. It is this third mechanism which I shall investigate.
| Adapted for the Internet from: Why God Doesn't Exist |
Fig. 1 Three ways that ‘length’ can ‘really’ contract in Physics: |
| a. Loss of a portion of the body b. Compression of the atoms that
c. Atoms of the body come closer
|
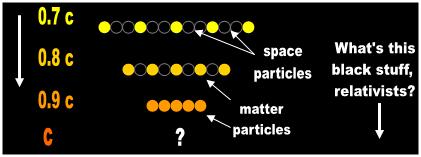
Fig. 2 Al’s vanishing distance particles |
Einstein’s machine-washed way simplifies my analysis enormously: the distance between atoms comprising the boy
decreases at the expense of space. However, this creates a bit of a problem because Mathematical Physics hypothesizes
that objects are mostly comprised of empty space:
- “ Ordinary matter, or the stuff we and everything around us is made of, consists
largely of empty space. Even a rock is mostly empty space.” [1]
“ A cloud of tiny negatively-charged electrons envelopes the nucleus, but at a
relatively large distance, so that much of the volume of an atom is empty space.” [2]
Mathematical Physics further holds that empty space is made of particles:
- “ Laboratory experiments show that seemingly empty space is actually seething with
virtual particles that wink in and out of existence.” [3]
“ the vacuum, which generally appears empty, is somehow packed out with electrons.”
(p. 102) [4]
“ Vacuum energy is an underlying background energy that exists in space even
when devoid of matter. The vacuum energy results in existence of most (if not all)
fundamental forces…vacuum fluctuations are always created as particle/antiparticle
pairs.” [5]
- Think of this (if you can) as ‘particles of distance’. In the quantum-relativistic universe, invisible spirits saturate the separation
between any two objects. Hence, in order for matter particles to come closer, they must necessarily dislodge invisible
quantum 'distance' particles from their ‘positions’ (Fig. 2).
SR’s length contraction theory requires matter particles to strain space particles out of the object as it contracts. |
I talk about relativity’s space particles in another page, so it would be redundant to repeat the reasons for rejecting physical
contraction on this basis. In order to make a different point, I will assume that space is what it really is – a true vacuum,
nothing – and thus leave space out of the discussion altogether. The particles of matter simply take up less volume (however
you want to visualize this!).
However, compression of matter under Al’s machine-washed version suffers from terminal illness. According to SR, the
constituent atoms also flatten out in the direction of motion of the object. The distance between the electrons and the
nucleus of each atom also decreases. In fact, the distances within protons, neutrons, quarks, and gluons should decrease
as well if these particles are made of smaller components. From a conceptual point of view, the only particle that cannot
compress further is a continuous, rigid, or elementary particle: a particle made of a single piece. A continuous particle is
conceptually devoid of pockets or bubbles of space and is therefore not amenable to compression at all. An elementary
or fundamental particle is by definition one which cannot be compressed.
Quantum Mechanics absolutely ‘predicts’ that there is such an indivisible particle. Quantum is based on the hypothesis
that irrespective of how many times you chop a particle into pieces, you always end up with pieces. It is irrational to say
that you cut something in half and end up with nothing on both sides of the knife.
One such fundamental particle candidate is the electron, which is said to have no internal structure down to a length of
10-16 cm. (p. 123) [6] If every atom contains at least 2 indivisible particles (one in the nucleus and another in the orbiting
electron), the aggregate of their diameters, and not Lorentz’s equation, provides a limit to how much an object can
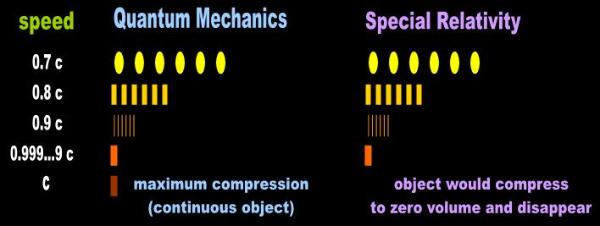
physically compress. Maximum compression implies that the object has somehow become continuous (Fig. 3), which
means that we no longer have discrete components. We have strained all the space bubbles from the object. It also
means that relativists have amended their initial assumptions: They constructed a continuous object with tinier indivisibles.
But we're not concerned about this contradiction right now. We are concerned that Special Relativity's contraction
equation predicts something different than Quantum Mechanics. The Lorentz-Fitzgerald contraction formula says that
as an object approaches the speed of light it continues to contract in proportion to its speed. If it could travel exactly at
the speed of light, it would disappear altogether. Quantum says, instead, that an object has a minimum diameter possible
below which it cannot possibly compress. This diameter is the sum of the diameters or lengths of the fundamental
particles that constitute the object (Fig. 3). As an example, assume that the elementary particle of Quantum has a diameter
equal to the Planck Length. If an object is comprised of five such particles in a row, the minimum length the object may
have is five Planck Lengths, and so on (Fig. 4). It doesn't matter how fast this object travels. It simply cannot compress
below what is the physical limit of its elementary constituents without violating logic.
Fig. 3 Al’s rigid contractions |
| SR predicts that particles of matter flatten out in the direction of travel and vanish altogether at c. QM predicts that maximum compression of the object is a function of the size of its indivisible components. So we encounter a contradiction in Mathematical Physics. Relativists are required to answer in addition: |
Incompressibility of a fundamental particle is the issue where SR and QM run up against each other. The SR length
contraction equation predicts that an object traveling at exactly c becomes so short that it vanishes. Here I have just
demonstrated that irrespective of how fast it travels or how many space bubbles we strain out of it, QM predicts that
an object will compress no further than the cumulative lengths of its elementary constituents. No amount of math will
overcome this objection. This is strictly a conceptual issue.
Hence, Einstein doesn’t have to worry about disappearing or turning into pure energy if he travels at c. At some point
below c, quantum logic predicts that the object becomes perfectly rigid and cannot compress further to satisfy the
requirements of Lorentz’s equation. It is not surprising, then, that Einstein could not visualize how the object disappears
altogether in the next frame (i.e., at c). By what mechanism do the mathematical physicists propose a subatomic ‘particle’
loses length, width, and height anyways? Unless they can answer this question, their equations are irrelevant. More to
the point, by what physical mechanism does mass convert to nothing or to energy if both mass and energy are concepts?
In fact, the ‘rigidity’ issue is relevant even before then. By what means or process does speed eliminate space within a
traveling object? What is it about speed (a process) that physically squeezes the living space (nothing) out of a boy
(an object)? Relativists can talk about measurement and formulas all they want, but until they can answer these
questions they have no physical justification to claim that an object contracts. This is what Physics is about: explaining
the physical mechanism. Anything else is just math and BS.
| 11. By what physical mechanism does speed compress matter? 12. How does speed remove the last vestiges of space to create a perfectly
single piece.
height? |


| I warned you that this would happen if you continued to dance at the speed of light. |
Pages in this module:
a. This page: QM’s ‘mother of all particles’ prevents SR’s ruler from disappearing if it travels at c
b. If objects flatten out only in the direction of travel, what happens in other directions?
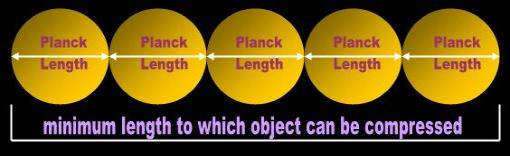
| Fig. 4 |
| Assume that the diameter of the fundamental or elementary particle predicted by QM is the Planck Length. If there is at least one such particle in an electron and another in the nucleus, the minimum size a hydrogen atom can be compressed is two Planck Lengths. If an object is comprised of five such elementary particles, the minimum size it can be compressed is five Planck Lengths. And so on. This 'prediction' of Quantum contradicts the prediction of Special Relativity that an object can continue compressing gradually until it almost disappears at near-c velocities. Relativists would otherwise have to explain in rational terms how a physical object spontaneously loses length, width, and height. |
- ________________________________________________________________________________________
- Copyright © by Nila Gaede 2008
