Adapted for the Internet from:

Why God Doesn't Exist
In Mathematics, there is no
such concept as distance

    The fact that the mathematicians measure ‘distance’ with a tape at times and at others with a clock indicates that they are not
    in the habit of discriminating between space and time:

    " we can use a more convenient, new unit of length called a light-second. This is
       simply defined as the distance that light travels in one second. In the theory of
       relativity, we now define distance in terms of time and the speed of light" (p. 23)  [7]

    " When an object undergoes displacement from one location to another, the distance
       traversed divided by the time elapsed is called the speed of the object.  
       (Speed = Distance/Time) " (p. 77) [8]

    " The distance between two points is the length of a straight line between them.
       Distance is sometimes expressed in terms of the time to cover it... 'distance from
       A to B' is interchangeable with 'distance between A and B'. "  [9]

    [What incongruous mixture! The distance between two points is a length which
     is the time to cover the distance!]

    When a mathematician specifies that the distance is ‘10 meters’ he is not referring to the empty space that separates two
    objects in the present. He is referring to the length of the real or imaginary tape that he just finished stretching between them.
    He is talking about something that happened in the past:

    " Displacement is a vector quantity which expresses the length and direction of a
       straight line from one place to another as opposed to the scalar quantity distance
       which expresses only the length. The SI unit for either distance or displacement is
       the meter." [10]

    As far as the mathematician is concerned, he has to unroll the tape whether he measures length or distance or displacement,
    so what the hell is the difference? To a mathematician, length, distance, and displacement are all the same. They are dynamic
    parameters, just numbers followed by units. In fact, it must be so in Mathematics! This discipline has no use for static
    concepts like the genuine length and distance of Physics. Unlike Physics, Mathematics is exclusively a dynamic field of study.

    Thus, the words length and distance of Mathematics are wolves in sheep's clothing. These words represent quantitative
    displacements. When a mathematician talks about length, or about distance, or about displacement, he is really counting tick
    marks on a clock. He is logging the rate at which he places tiles on a floor. In the idiotic religion of Mathematical Physics,
    length, distance, and distance-traveled are movies of something in motion (Fig. 1). That is why the mathematician alludes to a
    mathematical expression to specify and define distance:

    " the distance between two points of the xy-plane can be found using the distance
       formula" [11]

    An equation or function is a recipe that always gives you a single point. If you want to see a trend, you must replace the
    variables with different numbers. When a mathematician says that an equation depicts a distance, he is in effect asking you
    to replace the variables with numbers. He is talking about motion, about plotting 'points' on a chart, and not about a static gap
    that separates two objects. He is talking about 'proving; the definition of distance. Without a director or testimony or a video
    camera, Mathematical Physics is dead!

    So what do any of these definitions have to do with length and with the distance they just defined? What do these definitions
    have to do with Physics or with Science?

    Do not be misled by the 'scientific' sounding words. Make no mistake about it. These definitions belong in religion. They
    certainly are not 'rigorous.'

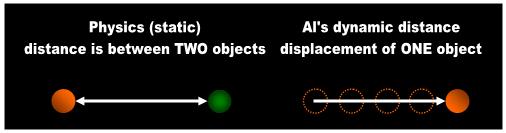
Fig. 2   Distance versus displacement
I'm trying to measure
the length of my land. I
think it is 843 jugs long!

    Therefore, whenever the morons of Mathematics utter the word distance, they are not referring to what the layman
    understands by distance. They are not talking about a snapshot of the empty space between their ears. They are talking
    about a film of a measurement. They are asking you to watch a movie of a tiny object streaking across the screen. The
    'distance' of Mathematics requires an observer. It requires a conscious witness to remember the initial location of the
    object and to compare it against the ending location. The 'distance' of Mathematics is naught without memory. The
    mathematical distance is not a photograph (distance between TWO objects), but a movie (a series of locations of ONE
    object) (Fig. 2). The common wisdom in Mathematical Physics is that everything can be reduced to measurement and
    measurement is, of course, depicted with a line:

    “Motions can be represented as lengths”  [12]

    That's how a displacement became a distance, which became a length, which became a line, which is really a point
    traveling from here to there. The mathematicians have blended so many irreconcilable concepts into their strategic
    definitions that these have become meaningless. The 'scholars' can explain anything with them and understand nothing.

Fig. 1   Math versus Physics
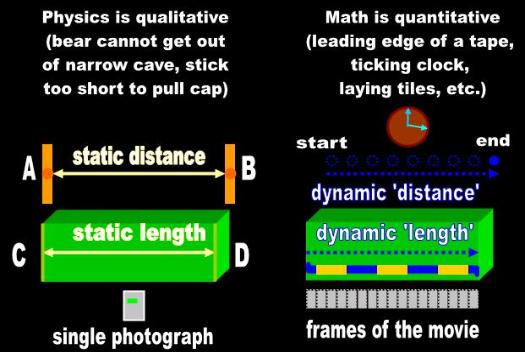
In Physics, length and distance are conceptually qualitative and static. We can freeze length
and distance in a single photograph. Both length and distance invoke TWO surfaces. We may
tentatively draw length and distance with solid lines to indicate that the image invokes a single
frame of the movie: a photograph. We draw TWO arrowheads at the ends of each of these lines
to indicate that length and distance extend between TWO surfaces. In this manner we don't
lose sight of the true meanings of these avatars and do not confuse them for the concepts
they represent.
In Math, length and distance are the distances traveled by the leading edge of a tape, the arm
of a clock, or another device used in the dynamic measurement process. The mathematician
is comparing the final location of ONE object against its now imaginary starting location. The
lengths and distances of Mathematics are expressed in terms of predefined units. We draw
distance-traveled with dotted, dashed, or segmented lines to indicate that we are pondering a
movie of a single object. The dots and dashes represent frames of the film. We draw ONE
arrowhead at the end of the line to indicate that only ONE object is involved.

Fig. 2
In Physics, distance is the (static)
separation between two surfaces.
You can only visualize this separation
laterally (horizontal distance).In contrast,
the distance-traveled of Mathematics is a
movie. The kinetic distance of Mathema-
tics consists of a stack of cards that an
observer fans in order to visualize motion
and can only be imagined in the direction
of travel. Conceptually, distance- traveled
is surrealistic because the mathematician
is attempting to sew from the present
location of the object to its imaginary
initial location through a stack of frames
comprising the movie. The object at its
initial location requires memory. There is
no real object there any more.   The
mathematical definition is unscientific
because it cannot be used consistently.

    2.0   Corollaries

    The establishment has never found a need to develop physical notions of length, distance, and displacement or to highlight
    their qualitative differences. The mathematicians have developed only subjective, measurement-related definitions of these
    terms. This explains, for example, why the ridiculous  Uncertainty Principle is still around in Quantum Mechanics. To a
    mathematician, the distance along the x-axis (what the idiots call 'position') is no different than if the particle would have
    traveled the same 'distance' (what they call 'momentum'). In QM, position is a dynamic parameter! In Mathematical Physics
    the word position means motion! There are no static concepts such as the genuine, qualitative location and position of
    Physics in Mathematics.

    Just as incongruous, relativists have taken the dynamic concept 'event' and converted it into a static object: an 'infinitesimal'
    dot (meaning, a location)! In Mathematical Physics, position means an event and an event is a position.


    3.0   Conclusions

    The mathematicians have utterly confused a static separation between TWO objects with the dynamic itinerary traced by
    ONE object. The mathematicians had no alternative but to use the definition of distance-traveled because they have always
    been in the business of measurement and measurement is a dynamic activity. The mathematician must roll out the tape and
    make a comparison with pre-established units. The distance of Mathematics is not a static, qualitative, spatial gap between
    two points. It is a magnitude measured in meters (number of tiles) or meters/second (rate at which the tile layer lays tiles).
    The mathematician first defines a standard such as the meter and then lays these tiles from one wall to another. For the last
    3000 years, the idiots of Mathematics have not only mistaken length for distance but then also confused separation (what is)
    with motion and time (what an observer measures). The distance-traveled notion of Mathematics is unscientific because it
    cannot be used consistently in a dissertation.
You see, Bill, at
Cambridge, we measure
length with a clock.
Mathematical 'length'

    1.0   Mathematicians don't use what they defined

    The mathematicians are famous for defining words very inadequately and then discarding what they defined and using
    something else during their presentations. The mathematicians begin their presentation by defining distance as length
    and length as distance. However, they don't use either of these notions anywhere in their presentations. What they use
    is distance-traveled, the itinerary of the leading edge of a measuring tape:

    “ Distance is a numerical description of how far apart things lie. In physics or
       everyday discussion, distance may refer to a physical length, a period of time,
       or an estimation based on other criteria (e.g. “two counties over”). In
       mathematics, distance must meet more rigorous criteria.”  [1]

    [Surely, you jest! The authors didn’t get anything right! Distance is not a numerical
     anything, it is not a length, it is not a period of time, and it is not an estimate. Where
     do the bozos who write in the Wikipedia go to school anyway? Harvard? But more
     offensive is the unjustified claim that Mathematics has rigorous definitions.]

    “ distance: For a particle with initial position x0, speed v, and acted upon by a
       constant acceleration a, the position as a function of time t is given by
       x = x0 + v0t + at2/2. The distance fallen under uniform acceleration a in order
       to reach a speed v is given by x = v2/2a.” [2]

    [This is the definition of distance? An equation? The morons of Mathematics don't
     define distance. They ‘prove’ the definition by running a test! The mathematicians
     are saying that you must accelerate a particle to know what distance is.]

    “ Whereas distances are always positive in Euclidean spaces, the distance
       between any two events in spacetime (called an ‘interval’) may be real, zero, or
       even imaginary. The spacetime interval quantifies this new distance (in
       Cartesian coordinates x,y,z,t)” [3]

    [Positive distance? Zero distance? Imaginary distance? The distance between
     two events? I wonder what the distance is between butt-scratching and nose-
     picking, two events that are happening right now over here!]

    “ Minkowskian ‘distance’ measured along the world-line describes the time that
       is actually experienced by that particle.” (p. 207)  [4]

    “ Time is the longest distance between two places.” [5]

    [Distance is time? So what is the distance between 2 a.m. and 3 p.m.?]

    “ The distance between two points on a number line…is the absolute value of the
       difference between their coordinates”  [6]

    [The distance on a number line? So what is the distance between the numbers
     4 and 7?]
Whatcha doin',
Newt?

    ________________________________________________________________________________________


                                  Home                    Books                    Glossary            




        Copyright © by Nila Gaede 2008