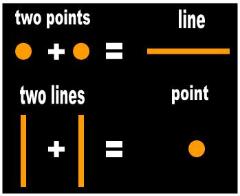
1.0   The two point line

    A hundred years ago, Hilbert decided to review Euclid's shaky axioms to put them on sounder footing.
    After many sleepless nights, he concluded that a line consists of two points:

    “ Two distinct points A and B always completely determine a straight line ... Any
        two distinct points of a straight line completely determine that line... Upon every
        straight line there exist at least two points" [1]

    Today, everyone in Mathematics repeats Hilbert's mantra by heart:

    “ First of all the straight line. Its distinguishing feature is that it is determined by two of
        its points.” (p. 12)  Every pair of points A and B determines a vector a… the end-points
        of all vectors OP …form a straight line." (p. 18)  [2]

    “ Lines are assumed to be straight unless otherwise defined and are determined by two
       specific points.”  [3]

    There are, however, insurmountable conceptual hurdles with the two bit line proposed by the
    mathematicians, among them:

    •        it relies on the undefined point
    •        it is a circular definition
    •        it is simultaneously finite and infinite
    •        it purports to build a continuous entity with discrete building blocks
    •        it is not a definition, but a proof


    2.0   The undefined point

    I held that the mathematicians have misconstrued the most fundamental figure of Geometry: the point.
    Nevertheless, the mathematicians freely admit that the infamous point is to this day an undefined geometric
    figure. Therefore, it seems that the mathematicians are off to an inauspicious start if they are attempting to
    define the word line by invoking the primitive point. For instance, if two points make a line, does it matter
    what a point looks like? Are the dimensions, sizes, and shapes of the points of no relevance (Fig. 1)?
Hilbert's two-bit line
Adapted for the Internet from:

Why God Doesn't Exist

    Of course, if a line can be both finite and infinite, we can see how the mathematicians can explain anything
    with it. This ambiguity comes in very handy when they 'prove' some of their geometric propositions.

    For instance, the mathematician begins his dissertation by telling you that a geometric figure is bound by
    lines:

    “ The area of the triangle formed by the three lines”  [11]

    This unscientific language is misleading. The mathematician is introducing ordinary speech in a scientific
    context. The correct term is line segment or just segment:

    “ a triangle consists of three line segments rather than of three lines; each side is the
       line segment between two vertices.”  [12]

    “ Lines are used to construct all other figures in plane geometry, including angles,
       triangles, squares, trapezoids, circles, and so on. Since a line has no beginning or
       end, most of the ‘lines’ one deals with in geometry are actually line segments —
       portions of a line that do have a limited length.”  [13]

    You may think that this is a trivial semantic issue. Okay. So the mathematician erred. He should have said
    line segment instead of line. So what?

    Ah, but this is not just a semantic issue! The mathematician now attempts to prove a theorem involving
    triangles. Does he use line segments? NO! He uses infinite lines. He stretches the line segment beyond the
    end point --  indeed, beyond the triangle --  and begins to construct angles on the outside of it. In fact, a
    mathematician works more on the outside than on the inside of a triangle.

    Okay. So the mathematician cheated a little. He started with a line segment. Now he stretches this allegedly
    finite line beyond the end point and converts it into an infinite line in order to prove a theorem. He
    constructed an angle on the outside of the triangle. Yeah. He broke the law a little, but this is quite harmless.
    The ends justify the means. We now can establish relations between internal and external angles and
    geometric figures.

    Wrong again! A triangle consists of three line SEGMENTS. What the idiot of Mathematics has done by
    stretching the segment is take his dissertation out of Geometry (Fig. 7). The mathematician has put us on
    notice that he is not interested in architecture. The mathematician is not talking about a geometric figure,
    but about a perimeter. A perimeter is all motion and no structure:

    “ The perimeter is the distance around a given two-dimensional object.” [14]

    [When a mathematician says distance, he means distance traveled. Mathematics has
      no use for qualitative concepts such as distance (i.e., a static gap between two
      objects). Mathematics is exclusively a dynamic discipline.]

    Therefore, the mathematician has now violated two rules. First, he stretched what he promised was
    unstretchable. Then, he is no longer talking about Geometry, a discipline that deals with static figures        
    (i.e., shapes). He is now talking about paces: a movie. The line of Mathematics grows at whim of the magic
    wand.  Are we now talking about a series of abstract locations, about a row of apples, or about  the distance
    separating two apples? Is the mathematician now referring to  a single apple rolling down the hill or to a
    bunch of footprints an apple marked in the sand? Is this line made of discrete entities or of a single piece?
    We cannot understand the mathematician until he tells us unambiguously what he means by point.

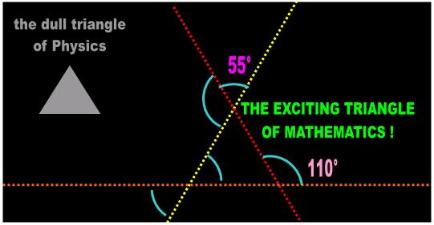
Fig. 7   The triangle of Physics against the triangle of Math.
A mathematician never uses the term
line segment except to clarify that it
means 'finite line'. Afterwards, he
dumps this concept into the trashcan
and always uses the word line to refer
to both.

This duality of the word line comes in
handy, for example, when proving
theorems and propositions. The
mathematician extends the line
segment forming a side of a triangle
and makes it infinite, meaning that he
doesn't specify where it ends. With the

    Another idiotic claim made by the mathematicians along these lines is that an arbitrary point on an infinite
    line divides the line in two equal rays. They are equal allegedly because there are still an infinite number of
    points on either side of the strategic point. You obviously cannot get away with making such ridiculous
    statements with a line segment.  

    The mathematicians are able to make such appalling claims because they don't have to produce the figure
    at the center of the dissertation. No one has measured to positive and negative infinity to certify whether the
    lengths are the same. They would never be able to do so because the infinite line is not a geometric figure.
    The infinite line is a movie with a very unhappy ending. Science and Physics do not recognize it as a valid
    exhibit because the proponent is not done with it. The infinite line is not about architecture, but about motion.
    It is a logical contradiction.


    5.0   The segmented, continuous line

    The mathematicians allege that a line is continuous yet that it is made of discrete points. They live at peace
    with this contradiction because our calculating friends have not defined the strategic words in their
    dissertation that allow them to get away with such preposterous claim.


    6.0   Proving a definition

    The two point line of mathematics is not a definition, but a proof. The ET has to wait until the mathematical
    trog finds another point in the woods to know what a line is. In Science, we don't prove definitions through
    an experiment. In fact, we don't even define physical objects. The only way to present a physical object in
    Science is by pointing to it and uttering a sound.


    7.0   Two numbers

    After the two hour presentation, the idiots of Mathematics tell you that they weren't talking about dots or
    points or even locations. They were referring to two numbers.

    “ the usual definition of distance between two real numbers x and y is:
       d(x,y) = |x − y|. This definition satisfies the three conditions above, and
       corresponds to the standard topology of the real line.” [15]

    So now it turns out that a line is the length, distance, or whatever lies between two numbers.

    "Granny? Please get my shotgun!"


    8.0   Conclusions

    Hilbert wasted his time reviewing Euclid's axioms. His modifications were cosmetic and didn't get to the
    heart of the matter. Hilbert changed absolutely nothing. His two bit line is not a part of Science because in
    the best of cases it merely tells us what a line is made of. Mentally sane human beings recognize a line when
    they see one. Not a single sane person on Earth will recognize two isolated points as a line, especially if we
    have not defined the number of dimensions of the point, their sizes, or their shapes.

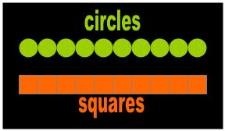
Fig. 2   Is a line made of circular/spherical dots or is it made of square/cubic dots?

Fig. 1   The two-bit lines of Mathematical Physics
If dimensions, sizes, and shapes of points are irrelevant to the construction of lines, I guess
I am authorized to use any combinations of these attributes to form my line. Which of the
pairs of dots below do you think your local mathematician would recognize as a line?
Can a series of circular dots form a straight
line? Can a row of spherical dots depict
concepts such as angle or parallel? These
geometric concepts require straight edges.
This summarily eliminates curved dots.

    To understand the relevance of these structural issues, consider that the mathematicians routinely make
    outrageous claims such as that there are ‘infinite’ points in a line segment:

    “ Given two distinct points A and C, there exists a point B on the line AC such that
       C lies between A and B." [4]

    “ Notice what a geometrical interpretation of the final conclusion could be: a line of
       infinite length (the real number line) has the same number of points as any finite line.” [5]

    “ In general, in any finite stretch of space, if space is continuous and real, there will be
       an infinite number of actual subregions all of finite size. (We're not talking about the
       points here: we're talking of regions of finite length.) So that's one example of an
       actual infinity.” [6]

    [ Regions don't have shape or sizes, but assuming they did, it is irrational to state that you
      can fit an 'infinite number' of them in a finite 'space'.]

    The mathematicians cannot get away with such ridiculous statements as long as they refuse to define the
    crucial word point unambiguously (Fig. 4). It is irrational for the prosecutor to present a dot, tell the jurors
    that his line consists of a series of dots, and then to switch to locations in the middle of the case and tell
    them that he can fit an infinite number of locations between any two dots or numbers between any two
    numbers. Either a point is a geometric dot or an abstract location. It can't be both.

    Another problem related to shape is that if the mathematician visualizes and illustrates a circular point, for
    example, he would not be able to use this point to build straight lines (Fig. 2) or concepts founded on straight
    lines: parallel, perpendicular, angle, etc. (Fig. 3) Conversely, if he presents a square point, the mathematician
    would not be able to build circles and spheres with it.

    Indeed, Weyl is probably one who visualized his lines as a bunch of contiguous squares. This would have
    been necessary for his lines to attain the property of straightness. I say ‘probably’ because there is not a
    single illustration of the dot he talks about in his entire book. The reader is supposed to guess what a point
    is or looks like. Weyl took for granted that his readers would know what he was talking about. Weyl could just
    as well have been imagining a point as a cube. The resulting line would have had a chance of being straight,
    but hardly 1-D.

    If the mathematician, instead, begins his presentation by equating a point with a location, then I am sorry
    but I have nothing to illustrate. A location without 'something' in it is absolutely nothing. It is irrational to talk
    about the size of a location. Under the 'location' variant of the word point, it would be impossible to visualize
    a line, and certainly the proposal would be divorced from Geometry.


    3.0   Circular definition

    The mathematicians claim that it takes two points to make a line:

    “ straight line... Its distinguishing feature is that it is determined by two of its
       points” (p. 12)  [7]

    When you look up the definition of point, you discover that it takes two lines to make a point. A point is
    defined as:

    “ Point: ...the intersection of two lines” [8]

    This is ironic because circularity is what the mathematician promised to avoid by not defining what he
    regards as a  primitive term. The mathematicians parrot what they are taught by rote in college without
    analyzing whether it makes any sense.   

    Fig. 4   Infinite dots between two dots?

Fig. 3

It is impossible to construct
straight-edge concepts such as
perpendicular, parallel, or angle with
round dots.
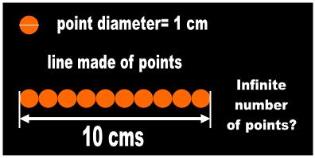
The mathematicians routinely boast that they
can fit an ‘infinite’ number of dots in a line
segment (i.e., a finite line). The rational mind
instantly protests. If I have a 10 cm line and
each dot is 1 cm in diameter, we can mathema-
tically fit only ten dots. We don't need to go to
college to realize this.

Fig. 5   Making a point
According to the jaw-dropping
logic of the mathematicians, it
takes two points to make a line,
but then also two lines to make
a point. So what have we
learned?

    4.0   The infinite, finite line

    The two point line also runs into trouble because the mathematicians define a line as being infinite:

    “ A line can be described as an ideal zero-width, infinitely long, perfectly straight
       curve containing an infinite number of points.” [9]

    Technically, it is a line segment that is bounded.

    “ a line segment is a part of a line that is bounded by two end points” [10]

    If two standalone points all by themselves constitute a line, presumably the line ends where the points end.
    This is a structural issue. If the (infinite) line continues to stretch beyond the points, what was the purpose of
    the two points? The mathematician is now describing an unspecified dynamic entity that is growing
    indefinitely, something like a balloon that is constantly filled with air.  These are two radically different
    characterizations. Either a line consists of two points or a line contains two points. The former would perhaps
    qualify as a definition of a line. The latter merely describes an attribute a line possesses.

    Fig. 6   Line vs. line segment
swift stroke of a magic wand the line segment suddenly begins to grow. By extending the segment
so casually and without justification, the mathematician tacitly insinuates that this not relevant to
the instant task of determining areas, angles, or whatever.

What he has really done, in his immense ignorance, is amend his initial assumptions. For instance,
does the word 'parallel' describe two lines or two segments? Do I have to convert two segments
into infinite lines to know whether they are parallel?

It turns out that, in Physics, a triangle is a standalone figure that consists of 3 straight edges. The
mathematicians are talking about something else. They are talking about perpetual motion. The
mathematicians are not the least concerned about architecture (i.e., triangles) They are concerned
about itineraries. The mathematical triangle is not a geometric figure. It has no body, no surface;
it is not a plane. The mathematical triangle is an abstract perimeter, a region bound by three
itineraries, a movie of a particle going around. This concoction has nothing to do with Geometry
or with Physics.

My argument may strike the reader as trivial and semantic. However, it becomes  relevant when
relativists use the same techniques to 'construct' space-time and wish you to believe that they are
describing the large scale structure of the Universe and that their discipline is founded on Geometry
when in fact relativity in its entirety only deals with locations and motion! Relativity has absolutely
nothing to do with Geometry or with Architecture! Mathematics is strictly a dynamic discipline.
That's a line?
Geez!
I guess
it must be all that
blood rushing to
his head.
This is how we construct a line
in Mathematics, Bill. We take
one point on our right and
another one on our left.
The trick used by the mathematician to peddle his snake oil is quite simple. He points to a
dot and shocks you with his outrageous claim. Your eyes are not deceived. It is an
impossible task. So you double dare him and place your bet. The mathematician waves
his magic wand, converts the dot into a non-dimensional location, calls it a number, and
explains that between any two numbers you can always find another one.

Huh? But I thought.... You said you would...

What does a dot have to do with a location, and what does either have to do with numbers.
How did we get from architecture and Geometry to abstract Math?

Indeed, what sense can it make to talk about physically fitting locations and numbers
between dots or locations or numbers? Is a location or a number a physical entity that can
be squeezed between two boxes? It is the incongruous language that the mathematicians
have invented and its inconsistent use that leads to the ridiculous conclusions of
Mathematics.
The mathematicians define a line
as infinite and a line segment as
finite. However, they self-servingly
use the word line to refer to both
the infinite line as well as to the
finite segment. This duality comes
in handy when pushing certain
theories.


    ________________________________________________________________________________________


                                  Home                    Books                    Glossary            




        Copyright © by Nila Gaede 2008